- UML2.1 – Học thống kê
- UML2.2 – Nguyên tắc cực thiểu rủi ro thực nghiệm
- UML2.3 – Cực tiểu hóa sai số thực nghiệm trên không gian giả thiết rút gọn
-
- Như chương trước đã đề cập, thuật toán học dựa vào tập dữ liệu \(S\) được lấy mẫu từ tập \(\mathcal D\) và được đánh nhãn bởi hàm \(f\), thuật toán này sẽ cho đầu ra là hàm \(h_S: \mathcal{X} \rightarrow \mathcal{Y}\) (kí hiệu \(h_S\) nhấn mạnh hàm dự đoán \(h_S\) chỉ phụ thuộc vào bộ dữ liệu \(S\)). Mục tiêu là cần tìm hàm \(h_S\) cực tiểu sai số của dữ liệu được sinh ra từ phân phối \( \mathcal D\) và hàm đánh nhãn \(f\).
- Do ta không biết được phân phối \(\mathcal D\) cũng như hàm đánh nhãn \(f\) vì thế chúng ta không thể tính được lỗi thật \(L_{D, f}\). Do đó để xấp xỉ, ta sử dụng lỗi trên tập dữ liệu huấn luyện (training error) để tính toán lỗi cho hàm dự đoán:
\(\begin{align}L_S(h) = \frac{|i \in [m] : h(x_i) \neq y_i|}{m}\end{align}\)
với \( [m] = \{1, \ldots, m\} \). Lỗi này còn được gọi là lỗi thực nghiệm (empirical error) hay rủi ro thực nghiệm (empirical risk). Vì tập dữ liệu huấn luyện được lấy mẫu trên phân bố thực tế \(\mathcal D\), cực tiểu hóa \(L_S(h)\) có thể làm giảm rủi ro kỳ vọng \(L_{D, f}\). Nguyên tắc này được gọi là cực tiểu rủi ro thực nghiệm, viết tắt là ERM (Empirical Risk Minimization).
- Mặc dù luật ERM có vẻ rất hợp lý, nhưng nếu sử dụng nó một cách bất cẩn, ta có thể gặp phải những lỗi sai lớn. Ví dụ, giả sử có bài toán dự đoán đu đủ xem một quả đu đủ đã chín hay chưa dựa vào 2 yếu tố (features) là độ mềm (softness) và màu sắc (color). Giả sử dữ liệu dữ liệu được mô tả như dưới hình vẽ sau:
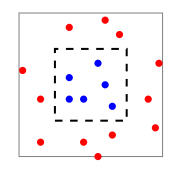
Giả sử phân phối \(\mathcal D\) là các dữ liệu được phân bố đều trong ô màu xám, hàm \(f\) gán nhãn 1 cho tất cả dữ liệu nằm trong hình vuông nét đứt (các điểm màu xanh), còn nhãn 0 là những điểm dữ liệu còn lại (màu đỏ). Diện tích hình vuông nét liền là 2, diện tích hình vuông nét đứt là 1. Nếu ta có hàm dự đoán \(h_S\) như sau:
\(\begin{align}h_S(x) = \begin{cases} y_i & \mbox{nếu } \exists i \in [m] \mbox{ sao cho } x_i = x \\ 0 & \mbox{các trường hợp còn lại}\end{cases} \end{align}\)
- Như vậy với bất kì mẫu \(S\) nào, hàm dự đoán \(h_S\) luôn có sai số trên tập huấn luyện \(S\) là 0. Theo nguyên tắc ERM, ta có thể chọn hàm dự đoán này vì hàm này có sai số thực nghiệm nhỏ nhất. Nhưng trên toàn bộ phân phối \(\mathcal D\) lỗi thực (rủi ro kỳ vọng) được tính trên những điểm dữ liệu có nhãn là 1, như vậy trong trường hợp này sai số thực tế là 1/2 (vì dữ liệu được phân bố đều).
- Như vậy, trong trường hợp trên, hàm dự đoán hoạt động rất tốt trên tập huấn luyện, nhưng trên bộ dữ liệu thực tế thì hoạt động rất kém, hay còn gọi thuật toán học bị học quá (overfitting).
